Grid searching data pipelines for wine quality

I collected a small set of crowd sourced wine data from the web to show how pipelines and grid search can be used together to run data analysis while being careful not to leak information from the test set into the training data.

##Load the data

data = response.json()  ## The data is in JSON format
df = pd.DataFrame(data)
df.head(10)

	Color	Consumed In	Country	Grape	Name	Price	Region	Score	Vintage	Vinyard
0	W	2015	Portugal				Portugal	4	2013	Vinho Verde
1	W	2015	France			17.8	France	3	2013	Peyruchet
2	W	2015	Oregon			20	Oregon	3	2013	Abacela
3	W	2015	Spain	chardonay		7	Spain	2.5	2012	Ochoa
4	R	2015	US	chiraz, cab	Spice Trader	6		3	2012	Heartland
5	R	2015	US	cab		13	California	3.5	2012	Crow Canyon
6	R	2015	US		#14	21	Oregon	2.5	2013	Abacela
7	R	2015	France	merlot, cab		12	Bordeaux	3.5	2012	David Beaulieu
8	R	2015	France	merlot, cab		11.99	Medoc	3.5	2011	Chantemerle
9	R	2015	US	merlot		13	Washington	4	2011	Hyatt

Split the data

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test, = train_test_split(X, y, test_size=0.2, random_state=42)

Set up classes for custom pipeline

class ModelTransformer(BaseEstimator,TransformerMixin):

    def __init__(self, model=None):
        self.model = model

    def fit(self, *args, **kwargs):
        self.model.fit(*args, **kwargs)
        return self

    def transform(self, X, **transform_params):
        return self.model.transform(X)
    
class SampleExtractor(BaseEstimator, TransformerMixin):
    """Takes in varaible names as a **list**"""

    def __init__(self, vars):
        self.vars = vars  # e.g. pass in a column names to extract

    def transform(self, X, y=None):
        if len(self.vars) > 1:
            return pd.DataFrame(X[self.vars]) # where the actual feature extraction happens
        else:
            return pd.Series(X[self.vars[0]])

    def fit(self, X, y=None):
        return self  # generally does nothing
    
    
class DenseTransformer(BaseEstimator,TransformerMixin):

    def transform(self, X, y=None, **fit_params):
#         print X.todense()
        return X.todense()

    def fit_transform(self, X, y=None, **fit_params):
        self.fit(X, y, **fit_params)
        return self.transform(X)

    def fit(self, X, y=None, **fit_params):
        return self

Run data with KFolds cross validation

kf_shuffle = StratifiedKFold(n_splits=3,shuffle=True,random_state=777)

binary = True
feats = 5

pipeline = Pipeline([
    ('features', FeatureUnion([
        ('Color', Pipeline([
                      ('text',SampleExtractor(['Color'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('Country', Pipeline([
                      ('text',SampleExtractor(['Country'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('Grape', Pipeline([
                      ('text',SampleExtractor(['Grape'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('Name', Pipeline([
                      ('text',SampleExtractor(['Name'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('Region', Pipeline([
                      ('text',SampleExtractor(['Region'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('Vinyard', Pipeline([
                      ('text',SampleExtractor(['Vinyard'])),
                      ('dummify', CountVectorizer(binary=binary, max_features=feats)),
                      ('densify', DenseTransformer()),
                     ])),
        ('cont_features', Pipeline([
                      ('continuous', SampleExtractor(['Consumed In', 'Price', 'Vintage'])),
                      ('impute',Imputer()),
                      ])),
        ])),
        ('scale', ModelTransformer()),
        ('tree', tree.DecisionTreeRegressor()),
])


parameters = {
    'features__Color__dummify__analyzer':['char'],
    'scale__model': (StandardScaler(),MinMaxScaler()),
    'tree__max_depth': (2,3,4,None),
    'tree__min_samples_split': (2,3,4,5),
}

grid_search = GridSearchCV(pipeline, parameters, verbose=False, cv=kf_shuffle)

Execute the pipeline

print("Performing grid search...")
print("pipeline:", [name for name, _ in pipeline.steps])
print("parameters:")
print(parameters)


grid_search.fit(X_train, y_train)

print("Best score: %0.3f" % grid_search.best_score_)
print("Best parameters set:")
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted(parameters.keys()):
    print("\t%s: %r" % (param_name, best_parameters[param_name]))


cv_pred = pd.Series(grid_search.predict(X_test))

Performing grid search...
('pipeline:', ['features', 'scale', 'tree'])
parameters:
{'tree__min_samples_split': (2, 3, 4, 5), 'tree__max_depth': (2, 3, 4, None), 'scale__model': (StandardScaler(copy=True, with_mean=True, with_std=True), MinMaxScaler(copy=True, feature_range=(0, 1))), 'features__Color__dummify__analyzer': ['char']}
Best score: 0.964
Best parameters set:
	features__Color__dummify__analyzer: 'char'
	scale__model: StandardScaler(copy=True, with_mean=True, with_std=True)
	tree__max_depth: 2
	tree__min_samples_split: 3

Take a peek at the results

pd.DataFrame(zip(grid_search.cv_results_['mean_test_score'],\
                 grid_search.cv_results_['std_test_score']\
                )).sort_values(0,ascending=False).head(10)

	0	1
17	0.963752	0.009070
1	0.963752	0.009070
20	0.958414	0.010273
13	0.955670	0.017514
15	0.955079	0.007642
27	0.955020	0.010817
6	0.954595	0.010570
26	0.952498	0.011002
9	0.838367	0.134405
22	0.835760	0.139155

grid_search.score(X_test,y_test) # prints the R2 for the best predictor

0.46448936196721591

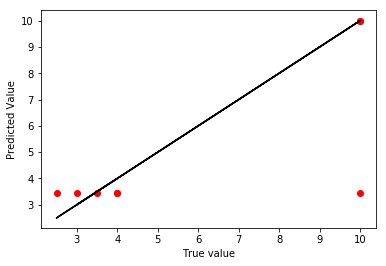
plt.scatter(y_test,cv_pred,color='r')
plt.plot(y_test,y_test,color='k')
plt.xlabel("True value")
plt.ylabel("Predicted Value")
plt.show()

png

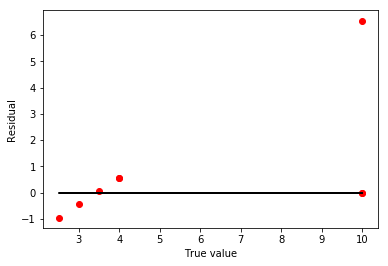
plt.scatter(y_test,y_test.values-cv_pred.values,color='r')
plt.plot(y_test,y_test-y_test,color='k')
plt.xlabel("True value")
plt.ylabel("Residual")
plt.show()

png

Results Summary

I was able to run a grid search on the data, and found that two models fit the training data equally well. When applied as a predictor on the test set, I get an R-squared value of 46.4%. Looking at the plots, I seem to be over fit and predicting a wild outlier at the right side. There is also a linear pattern to my residuals from one model, but the small sample size makes it hard to predict if that is by chance.

Written on May 10, 2017